Solar Physics

(2004) 224: 37–47 _

C Springer 2005

Review Paper

LONG-TERM SOLAR ACTIVITY: DIRECT AND INDIRECT STUDY

I. G. USOSKIN1 and G. A. KOVALTSOV2

1Sodankyl¨a Geophysical Observatory (Oulu unit), University of Oulu, P.O. Box 3000,

FIN 90014, Finland

2Ioffe Physical-Technical Institute, St. Petersburg 194021, Russia

(e-mail: ilya.usoskin@oulu.fi)

(Received 1 September 2004; accepted 23 September 2004)

Abstract. The series of directly observed sunspot numbers is nearly 400 years long. We stress that

the recently compiled group sunspot number series is an upgrade of the old Wolf series and should

always be used before 1850. The behavior of solar activity on longer time scales can be studied

only using indirect proxies. Such proxies as aurorae occurrence or naked-eye sunspot observations

are qualitative indicators of solar activity but can be hardly quantitatively interpreted. Cosmogenic

isotope records provide a basis for quantitative estimate of the past solar activity. Here we overview

the main methods of the long-term solar activity reconstruction on the centennial to multimillennia

time scale. We discuss that regression-based reconstructions of solar activity lead to very uncertain

results, while recently developed physics-based models raise solar activity reconstruction to a new

level and allow studying its behavior on a multimillennia time scale. In particular, the reconstructions

show that the recent episode of high solar activity is quite unusual in the multimillennia time scale.

1. Introduction

The sunspot number (SN) series is the longest record of directly observed solar

activity, which started in 1610 and covers about 400 years. During this period

SN was varying between the nearly spotless Maunder Minimum and the recent

unusually high activity when SN reached the average value of about 75. The main

features of solar activity on the decennial–centennial time scale were summarized,

e.g., by Vitinsky (1986) or Usoskin and Mursula (2003). However, it is important to

know the behavior of solar activity on even longer time scales for many reasons, in

particular for the solar/stellar dynamo theory and for research on long-term solarterrestrial

relations (“space climate”). Since there were no regular observations in

the pre-telescopic era, indirect methods are used for the purpose. Here we overview

the main methods and results of the long-term solar activity reconstruction on the

centennial to multimillenial time scale.

2. Sunspot Number Series

Until recently the longest series of sunspot observations was the famous Wolf

sunspot number (called WSN henceforth) which was primarily compiled by Rudolf

38 I. G. USOSKIN AND G. A. KOVALTSOV

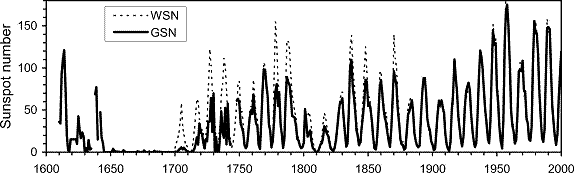
Figure 1. The annual series of sunspot numbers: Group sunspot numbers (GSN, solid line) andWolf

sunspot numbers (WSN, dotted line).

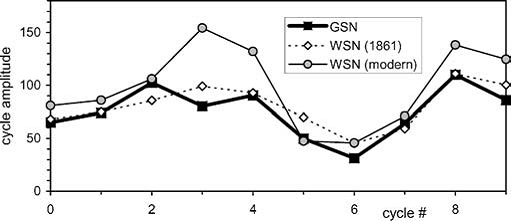
Figure 2. The amplitude of solar cycles according to GSN (thick lines and black squares), original

WSN published in 1861 (dotted line with open diamonds) and the corrected “modern” WSN (thin

line with grey dots).

Wolf of Z¨urich Observatory and then continued using the same method (Waldmeier,

1961) (since the 1980s WSN is provided by the Royal Observatory of Belgium).

The official WSN starts in 1749, and before that only yearly WSN values are

available (Figure 1). The WSN series uses only one (primary) observer for each

day with all gaps being interpolated without notes (for details see, e.g., Hoyt and

Schatten, 1998). Therefore, the WSN series is a combination of direct observations

and interpolations for the period before 1849 with all the raw information hidden,

which makes it impossible to estimate its uncertainties (see, e.g., Vitinsky et al.,

1986; Hoyt et al., 1994; Wilson, 1998; Letfus, 1999). WSN contains not only

sunspot but also geomagnetic data as illustrated by Figure 2. After publishing his

original sunspot series in 1861 (Wolf, 1861),Wolf corrected it using the “magnetic

needle” (geomagnetic inclination range) data measured in Milano (see the full story

in Hoyt and Schatten, 1998). Note that the original WSN series is much closer to

the Group spot numbers (GSN) than the corrected WSN which is widely used now.

Thus, the WSN series can be analyzed only for the period since 1849 or, with

caveats, since 1749.

Recently a new updated sunspot series, called the Group sunspot number (GSN)

series (see Figure 1), was presented by Hoyt and Schatten (1998), which contains

80% more raw information and is more homogeneous than WSN (Hoyt and

LONG-TERM SOLAR ACTIVITY: DIRECT AND INDIRECT STUDY 39

Schatten, 1998; Letfus, 1999; Hathaway et al., 2002). Although GSN still contain

some uncertainties, it is important that all raw information is available which

allows for independent re-analysis, error estimate, and statistical studies (Usoskin

and Mursula, 2003). The GSN series is strongly recommended for analysis of

sunspot activity before 1850. It should be noted that WSN and GSN are not different

alternative proxies of solar activity but rather GSN is an upgrade of the WSN

series. We note that even GSN series is not finalized, and new archival results on

sunspot observations appear, filling some gaps in GSN (Vaquero, 2004).

3. Indirect Proxy

The only way to study solar activity in the pre-telescopic era is related to the so

called indirect solar proxies.

Such a proxy is the record of visual observations of aurorae borealis in middlelatitudes

which are caused by enhanced geomagnetic activity due to transient interplanetary

phenomena (e.g., Schove, 1983; Silverman, 1983, 1992, 1998; K˘rivsk´y

and Pejml, 1988). Fragmentary records of aurorae can be found in Occidental and

Oriental sources since antiquity. These data are sensitive to long-term changes of

the geomagnetic field. Also, because of the phenomenon’s short duration and low

brightness, the probability of seeing aurora can be affected by a number of factors

(clouds, the phase of the Moon, season, etc.). The fact that these observations were

not systematic in early times makes it difficult to produce a homogeneous data set.

Some fragmentary data on naked-eye observations of sunspots exist for quite

early times, mostly from Oriental sources (see, e.g., Clark and Stephenson, 1978;

Wittmann and Xu, 1987; Yua and Stephenson, 1988). Spots on the Sun are mentioned

in official Chinese and Korean chronicles from 165 BC to 1918 AD. While

these chronicles are fairly reliable, these data are not straightforward to interpret

since they can be influenced by meteorological or other phenomena (e.g., dust loading

in the atmosphere due to dust storms or volcano eruptions facilitates sunspot

observations). Moreover, records of sunspot observations in the official chronicles

depended on the dominant traditions during specific historical periods. Direct comparison

of the Oriental naked-eye sunspot observations and European telescopic

data shows that the naked-eye observations can serve only as a qualitative indicator

of the sunspot activity but can be hardly quantitatively interpreted (see, e.g.,Willis,

1996 and references therein).

The most useful proxy of solar activity is formed by the data on cosmogenic

radionuclides, e.g., 10Be and 14C, which are produced by cosmic rays in the Earth’s

atmosphere (e.g, Stuiver and Quay, 1980; Beer et al., 1990; Bard, 1997; Beer, 2000).

Cosmic rays are the major source of cosmogenic nuclides in the atmosphere (excluding

anthropogenic factors during last decades) with the maximum production being

in the upper troposphere/stratosphere. After a complicated transport in terrestrial

reservoirs (atmosphere, ocean, biosphere) they are stored in natural archives such

40 I. G. USOSKIN AND G. A. KOVALTSOV

as polar ice, trees, marine sediments, etc. Because of the heliospheric modulation

of the cosmic ray intensity at the Earth’s orbit, the cosmogenic isotope production

depends inversely on solar activity. An important advantage of the cosmogenic

data is that primary archiving is done routinely in a similar manner throughout

the ages, and these archives are measured nowadays in laboratories using modern

techniques. If necessary, all measurements can be repeated and improved as has

been done for some radiocarbon samples. In contrast to fixed historical archival

data (such as sunspot or auroral observations) this approach, together with absolute

independent dating of samples, allows for homogeneous data sets with stable

quality. Cosmogenic isotope data are the only regular indicator of solar activity on

the very long-term scale but they cannot always resolve details of individual solar

cycles. Redistribution of the nuclides in the terrestrial reservoirs and archiving may

be affected by local and global climate/circulation processes which are to a large

extent unknown in the past. However, a combined study of different nuclides data,

whose responses to terrestrial effects are very different, may allowfor disentangling

external and terrestrial signals.

4. Solar Activity Reconstruction from Proxy Data

4.1. MATHEMATICAL METHODS

There are numerous attempts to extend the sunspot series back in time using

extrapolations of its statistical properties (e.g., De Meyer, 1998; Rigozo et al.,

2001). Actually, it is not a reconstruction based upon measured or observed quantities

but rather a “post-diction.” Although often used for predictions, such a method

can hardly be applied for a reliable reconstruction of solar activity. In particular, it

assumes that the time series is stationary, i.e. that all information on its future/past

is contained in a limited time sample. Clearly such models cannot include periods

exceeding the time span of observations upon which the extrapolation is based.

Regressions are the most used method of solar activity reconstruction from

proxy data (see, e.g., Stuiver and Quay, 1980; Ogurtsov, 2004).Aphenomenological

regression (either linear or nonlinear) is built between proxy data set and the directly

measured solar activity for the available “training” period (since 1750 for WSN or

since 1610 for GSN). Then this regression is extended backwards to evaluate SN

from the proxy data. The main shortcoming of the regression is that this method

depends on the time resolution and “training” period. The former is illustrated by

Figure 3 which shows the scatter plot of the 10Be concentration vs. GSN for the

annual and 11-year smoothed data. One can see that the slope of the 10Be-vs.-GSN

relation within individual cycles is significantly different (about−500 g/at) from the

slope of long-term relation (about−100 g/at), i.e., individual cycles do not lie along

the line of 11-year averaged cycles. Therefore, the formal regression built using

the annual data for 1610–1985 yields a much stronger GSN-vs.-10Be dependence

LONG-TERM SOLAR ACTIVITY: DIRECT AND INDIRECT STUDY

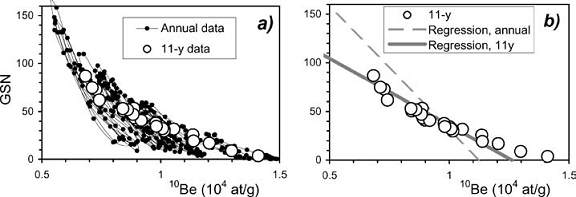
Figure 3. Scatter plot of smoothed group sunspot numbers vs. (2-year delayed) 10Be concentration.

(a) Annual (connected small dots) and 11-year averaged (big open dots) values. (b) Best-fit linear

regressions between the annual (dashed line) and 11-year averaged values (solid line). The dots are

the same as in panel (a).

than for the cycle-averaged data (see Figure 3b). Accordingly, when applying an

annual-based regression to the long-term smoothed 10Be (and other proxy) data

may result in erroneous evaluation of the sunspot number. Also, the use of WSN

instead of GSN before 1850 to build a regression can lead to additional errors in the

reconstruction, since WSN overestimates the SN level for the eighteenth century

(Section 2). We note that earlier regression works (before 1998 when Hoyt and

Schatten published their final GSN series) were based on WSN series and should

be revised.

Sometimes a fit of a mathematical model to indirect proxy data is used, which

is a combination of the extrapolation and proxy methods. In such models a mathematical

extrapolation is fitted to some proxy data for the time when direct data

are not available, e.g., Schove (1955) fitted the slightly variable but phase-locked

carrier frequency (about 11 years), to fragmentary data from naked-eye sunspot

observations or auroral sightings. This approach has been recently modified using

nonlinear relations (Nagovitsyn, 1997), but its shortcomings still limit the reliability

of the reconstruction. We note that these works yield too high sunspot activity

during the Maunder minimum.

4.2. PHYSICS-BASED MODELS

Anew step in long-term solar activity reconstruction has been made recently, which

is a development of the proxy method where physics-based models are used, instead

of a phenomenological regression, to link SN with the cosmogenic isotope

production (Beer et al., 2003; Usoskin, 2003; Solanki, 2004). Due to recent theoretical

developments, it is now possible to construct the chain of physical models

to simulate the entire link between solar activity and cosmogenic data. The first

model (Solanki, 2000, 2002) relates the open solar magnetic flux to SN (through

42 I. G. USOSKIN AND G. A. KOVALTSOV

the magnetic flux in sunspots). Although this model is based on physical principles,

it contains one adjustable parameter, the decay time of the open flux, which cannot

be measured or theoretically calculated and has to be found fitting the model to

data. Open flux data since 1975 were used to fix this parameter (Solanki et al.,

2000, 2002). The open magnetic flux is directly related to the global interplanetary

magnetic field which modulates the spectrum of cosmic rays at the Earth’s

orbit. The next model (Usoskin et al., 2002a) calculates the cosmic ray spectrum

X(P,_), where _ is the heliospheric modulation strength and P is particle’s rigidity,

from the open magnetic flux. For studies of long-term changes of the cosmic

ray flux, the parameter _ alone adequately describes the modulation of the cosmic

ray (Caballero-Lopez and Moraal, 2004). The connection between the cosmogenic

isotope production rate, Q, at a given location and the cosmic ray flux is given by

Q(θ) = _ ∞

Pc(θ)

X(P,_) · Y (P)dP, (1)

where θ is the geomagnetic latitude, Pc is the local cosmic ray rigidity cutoff,

and Y (P) is the differential yield function of cosmogenic isotope production (see

Castagnoli and Lal (1980) for 14C, and Masarik and Beer (1999) or Webber and

Higbie (2003) for 10Be). The abundance of 10Be in polar ice is assumed to be

directly proportional to its atmospheric production rate (Beer et al., 1990, 2003;

Masarik and Beer, 1999; Usoskin et al., 2002a) owing to its short residence time

in the atmosphere and relatively simple precipitation process. On the other hand,

a complicated global carbon cycle is involved between the production of 14C in

the atmosphere and its final deposition in tree rings (see, e.g., Damon et al., 1978;

Stuiver and Quay, 1980). Because of the global nature of the carbon cycle and its

long attenuation time, the radiocarbon is globally mixed before the final deposition,

and Equation (1) should be integrated over the globe. Thus, a physics-based model

exists for every step linking the solar activity to cosmogenic isotope content. The

validity of this link was verified by Usoskin et al. (2002b) who calculated the

expected concentration of 10Be in polar ice from the GSN record and showed that

it corresponds well to the measured concentration.

Inverting the physics-based model one can quantitatively evaluate the solar activity

from the measured cosmogenic isotope abundance. Due to strong nonlinearity

of the model, its inversion cannot resolve individual 11-year cycles, and only cycleaveraged

slow changes of the solar activity can be reconstructed (Usoskin et al.,

2003, 2004). Using the data on 10Be measured in Greenland and Antarctic ice,

Usoskin (2003) reconstructed 11-year averaged SN since 850 AD (Figure 4). This

result reproduces the four known grand minima of solar activity – Maunder (1645–

1715), Sp¨orer (around 1500 AD), Wolf (around 1300 AD), and tiny Oort (around

1050 AD) minima (cf., e.g., Peristykh and Damon, 2003). Later Solanki et al. (2004)

reconstructed 10-year averaged sunspot numbers from the 14C content in tree-rings

throughout the Holocene and estimated its uncertainties (see Figure 4). The slightly

negative values during the grand minima are an artifact, they are compatible with

LONG-TERM SOLAR ACTIVITY: DIRECT AND INDIRECT STUDY 43

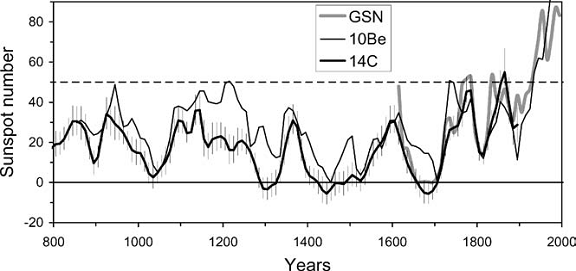
Figure 4. 10-year averaged sunspot numbers: Actual group sunspot numbers (thick grey line) and the

reconstructions based on 10Be (thin curve, Usoskin, 2003b) and on 14C (thick curve with error bars,

Solanki, 2004). The horizontal dotted line depicts the high activity threshold, 50.

the absence of sunspots within the error bars. One can see that the two SN reconstructions

are consistent with each other, but with the 10Be-based one being

systematically higher, especially in the early part of the millennium. This is expected

since Usoskin (2003) evaluated the upper limit of SN assuming the purely

local production of 10Be deposited in polar ice. Similar physics-based approach

was used by Beer et al. (2003) who also reconstructed the solar activity on the multimillennia

time scale using the 10Be data from GISP2 core in Greenland. They did

not reconstruct SN but presented the reconstructed modulation strength _ skipping

the last step in the physics-based model inversion, which may introduce additional

uncertainties. The two reconstructions, based on 10Be (Beer et al., 2003 – these

results are still preliminary) and on 14C (Solanki et al., 2004) data, are similar to

each other (J¨urg Beer, personal communication). Taking into account that the two

models are independent and use different isotopes with different geochemical fate,

this verifies the reliability of the long-term solar activity reconstruction.

4.3. VERIFICATION OF RECONSTRUCTION MODELS

As a verification of a SN reconstruction, its comparison with the actual GSN data

for the last centuries is usually used. However, regression-based models cannot be

tested in thisway since thiswould require long set of independent direct data outside

the “training” interval. It is usual to include all available data into the “training”

period to increase the statistics of a regression, which rules out a possibility to test

the model data. On the other hand, such a comparison to the actual GSN since 1610

can be regarded as a direct test for a physics-based model since it does not include

phenomenological relation over the same interval (the only adjustable parameter in

the model by Solanki et al. (2000) was fixed using data for 1975–2002). The period

44 I. G. USOSKIN AND G. A. KOVALTSOV

of the last four centuries is pretty good for the testing purpose since it includes

the whole range of solar activity from nearly spotless Maunder minimum to the

modern period of very active Sun. The agreement between the measured GSN

and the 14C-based reconstruction is excellent (the correlation coefficient r = 0.93

with the RMS deviation between the two series being 6) for the period 1610–1900

(Solanki et al., 2004). The agreement between GSN and 10Be-based reconstruction

(Usoskin, 2003b) is also good (r = 0.78,RMS=10 for 1700 –1985). This validates

the reliability of the physics-based reconstruction.

Note that both mathematical and physics-based models use an assumption on

the constancy of involved processes over the studied time scale. However, they

may change significantly through the ages. On the centuries-millennia time scale,

the most important changes are long-term changes of the geomagnetic field, when

both the geomagnetic dipole momentum changes and the dipole axis migrates (see,

e.g., Hongre, 1998). These changes modify the global shielding from cosmic rays,

changing thus the relation between SN and cosmogenic proxies. This may also

distort interpretation of the frequency of aurorae watching in the past. While geomagnetic

changes may distort the phenomenological reconstruction of sunspot

activity from proxy data, the physics-based model can naturally account for the geomagnetic

changes. Generally speaking, changes in the climate at the observational

site may also affect the solar activity reconstruction. However, the global climate

is known to be pretty stable during the Holocene (the present warm period lasting

for about ten millennia).

5. Solar Activity on the Multimillennium Scale

Some features of the very long-term solar activity, such as the occurrence of grand

minima, can be studied directly from cosmogenic isotope data, e.g.,Voss (1996) and

Peristykh and Damon (2003) analyzed the filtered _14C data for the last millennia

and demonstrated the existence of the secular (known also as Gleissberg) cycle and

the 200–210-year (de Vries or Suess) cycle throughout the studied intervals. Also,

a characteristic time of about 2000–2400 years was found in the frequency of grand

minima occurrence (Vasiliev and Dergachev, 2002; Peristykh and Damon, 2003).

Although this method is applied to an analysis of grand minima and qualitative

behavior of solar activity, it cannot study the quantitative level of the activity. On the

other hand, physics-based models (Section 4.2) provide quantitative reconstructions

of solar activity which allow studying also long-term changes in the activity and,

in particular, occurrence of periods with very high activity. The modern period of

high solar activity with the average SN of about 76 after 1940 is known, from the

direct observations, to be unique since 1610. Moreover, it was shown by Usoskin

(2003b), who used a physics-based SN reconstruction from 10Be data, that never

during the last millennium was the Sun as active as it has been since 1940, while the

cycle-averaged SN did not exceed the value of 50 for the millennium before that

LONG-TERM SOLAR ACTIVITY: DIRECT AND INDIRECT STUDY 45

Figure 5. Periods of solar activity extremes according to the reconstruction by Solanki et al. (2004).

Lower panel: grand minima, corresponding to reconstructed Rg < 10. Upper panel: periods of high

activity, corresponding to reconstructed Rg > 50 and Rg > 75, as denoted in the right.

(see Figure 4). However, the multimillennia physics-based reconstruction using

14C data (Solanki et al., 2004) suggests that the present high-activity episode is

not unique but rare on the multimillennia time scale, with several similar episodes

appearing 8,000–10,000 years ago.

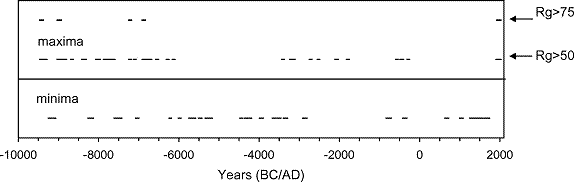
Figure 5 shows the periods of solar activity extremes. The lower panel depicts

grand minima which are defined as periods when the reconstructed 10-year averaged

SN did not exceed the value of 10 during at least 20 years. These periods are

close to earlier reconstructions of grand minima periods (see, e.g., Figure 2 in

Voss, 1996, who used raw _14C data). The characteristic time of 2000–2400-year

corresponding to clustering of grand minima is clear, while Gleissberg and de

Vries (Suess) periodicities in the grand minima occurrence can be traced within the

clusters. The most interesting is the upper panel of Figure 5 which shows the periods

of high solar activity, according to the reconstruction by Solanki (2004), defined

as a systematic (during at least 20 years) excess of SN over the given threshold

level. Here we show active periods for the two threshold levels, 50 and 75. Periods

when SN level exceeds 50 correspond to high solar activity. The latest (before the

present one) such episode had happened about 2400 years ago, implying again that

the modern episode is quite unique (SN level did not exceed 40 during the famous

Medieval maximum in twelfth century). The total number of such episodes is about

30 although they are not uniformly distributed – they tend to cluster around 500

BC, 1500 –3500 BC, and before 6000 BC. The threshold level of 75 corresponds

to extremely high activity episodes. There are only five such extreme episodes

(including the present one), four of which occurred before 6500 BC.

6. Concluding Remarks

We have presented a brief reviewof methods and results in studying long-term (from

centennial to multimillennium time scales) solar activity which can be summarized

as follows. Group sunspot numbers should be used instead of theWolf series for the

46 I. G. USOSKIN AND G. A. KOVALTSOV

times before 1850. The use of a linear regression to reconstruct solar activity yields

very uncertain results. Recently developed physics-based models raise solar activity

reconstruction to the newlevel and allowstudying its behavior on the multimillennia

time scale. The frequency of the occurrence of extremes of solar activity is analyzed

using SN reconstruction by Solanki et al. (2004). The characteristic time of 2000–

2400-year as well as Gleissberg and de Vries (Suess) periodicities are apparent in

the grand minima occurrence. It is important to note that the modern episode of

very high solar activity (after 1940) is very rare in the multimillennia time scale,

through the entire Holocene. There were only four other similar episodes, all of

them occurred before 6500 BC.

We would like to see further investigations in the following directions. New

measurements of cosmogenic proxies will help disentangle the terrestrial and solar

signals. The physical models discussed here should be improved with more realistic

consideration of changing geomagnetic and climatic factors. A systematic search

for historical information on sunspot observation may resolve some uncertainties

in sunspot activity during, e.g., the eighteenth century.

Acknowledgements

We thank J¨urg Beer for useful discussions. We acknowledge financial support by

the Academy of Finland.GAKwas partly supported by the program “Nonstationary

processes in Astronomy” of the Russian Academy of Sciences.

References

Bard, E., Raisbek, G. M., Yiou, F., and Jouzel, J.: 1997, Earth and Planet. Sci. Lett. 150, 453.

Beer, J.: 2000, Space Sci. Rev. 94, 53.

Beer, J., Blinov, A., Bonani, G., Finkel, R. C., Hofmann, H. J., Lehmann, B., Oeschger, H., Sigg, A.,

Schwander, J., Staffelbach, T., Stauffer, B., Suter, M., andWolfli,W.: 1990, Nature 347, 164–166,

1990.

Beer, J., Vonmoos, M. V., Muscheler, R., McCracken, K. G., Mende, W.: 2003, Proc. 28th Internat.

Cosmic Ray Conf. 7 Tsukuba, 4147.

Caballero-Lopez, R. A. and Moraal, H.: 2004, J. Geophys. Res. 109(A1), A01101, doi:

10.1029/2003JA010098.

Castagnoli, G. and Lal, D.: 1980, Radiocarbon 22(2), 133.

Clark, D. H. and Stephenson, F. R.: 1978, Q. J. R. Astr. Soc. 19, 387.

Damon, P. E., Lerman, J. C., and Long, Au.: 1978, Ann. Rev. Earth Planet. Sci. 6, 457.

De Meyer, F.: 1998, Solar Phys. 181, 201.

Hathaway, D. H., Wilson, R. M., and Reichmann, E. J.: 2002, Solar Phys. 211, 357.

Hongre, L., Hulot, G., and Khokhlov, A.: 1998, Phys. Earth Planet. Inter. 106, 311.

Hoyt, D. V., Schatten, K. H., and Nesme-Ribes, E.: 1994, Geophys. Res. Lett. 21, 2067.

Hoyt, D. V. and Schatten, K., 1998: Solar Phys. 179, 189.

K˘rivsk´y, L. and Pejml, K.: 1988, Astron. Inst. Czech. Acad. Sci. 75, 32.

Letfus, V.: 1999, Solar Phys. 184, 201.

Masarik, J. and Beer, J.: 1999, J. Geophys. Res. 104(D10), 12099.

LONG-TERM SOLAR ACTIVITY: DIRECT AND INDIRECT STUDY 47

Nagovitsyn, Yu. A.: 1997, Astron. Lett. 23, 74.

Ogurtsov, M. G.: 2004, Solar Phys. 220, 93.

Peristykh, A. N. and Damon, P. E.: 2003, J. Geophys. Res. 108(A1), 1003, SSH 1-1, doi:10.1029/

2002JA009390.

Rigozo, N. R., Echer, E., Vieira, L. E. A., and Nordemann, D. J. R.: 2001, Solar Phys. 203, 179.

Schove, D. J.: 1955, J. Geophys. Res. 60, 127.

Schove, D. J.: 1983, Annales Geophysicae 1, 391.

Silverman, S. M.: 1983, J. Geophys. Res. 88(A10), 8123.

Silverman, S. M.: 1992, Rev. Geophys. 30(4), 333.

Silverman, S. M.: 1998, J. Atm. Solar-Terr. Phys. 60, 997.

Solanki, S. K., Sch¨ussler, M., and Fligge, M.: 2000, Nature 408, 445.

Solanki, S. K., Sch¨ussler, M., and Fligge, M.: 2002, Astron. Astrophys. 383, 706.

Solanki, S. K., Usoskin, I. G., Kromer, B., Sch¨ussler, M., Beer, J.: 2004, Nature 431(7012).

Stuiver, M. and Quay, P.: 1980, Science 207, 11.

Usoskin, I. G., Mursula, K., Kovaltsov, G. A.: 2001, Astron. Astrophys. 370, L31.

Usoskin, I. G., Alanko, K., Mursula, K., Kovaltsov, G. A.: 2002a, Solar Phys. 207, 389.

Usoskin, I. G., Mursula, K., Solanki, S., Sch¨ussler, M., Kovaltsov, G. A.: 2002b, J. Geophys. Res.

107(A11), SSH 13-1, doi: 10.1029/2002JA009343.

Usoskin, I. G. and Mursula, K.: 2003a, Solar Phys. 218, 319.

Usoskin, I. G., Solanki, S., Schuessler, M., Mursula, K., Alanko, K.: 2003b, Phys. Rev. Lett. 91(21),

211101.

Usoskin, I. G., Mursula, K., Solanki, S., Schuessler, M., Alanko, K.: 2004, Astron. Astrophys. 413,

745.

Vaquero, J. M.: 2004, Solar Phys. 219, 379.

Vasiliev, S. S. and Dergachev, V. A., 2002: Annales Geophys. 20, 115.

Vitinsky, Yu. I., Kopecky, M., and Kuklin, G. V.: 1986, Statistics of Sunspot Activity, Nauka, Moscow,

Russia.

Voss, H., Kurth, J., and Schwarz: 1996, J. Geophys. Res. 101(A7), 15637.

Waldmeier, M.: 1961, The Sunspot Activity in the Years 1610–1960, Zurich Schulthess and Company

AG, Z¨urich, Switzerland.

Webber, W. R. and Higbie, P. R.: 2003, J. Geophys. Res. 108(A9), SSH 2-1, doi:10.1029/

2003JA009863.

Willis, D. M., Davda, V. N., Stephenson, F. R.: 1996, Q. J. R. Astr. Soc. 37, 189.

Wilson, R. M.: 1998, Solar Phys. 182, 217.

Wittmann, A. D. and Xu, Z. T.: 1987, Astron. Astrophys. Suppl. Ser. 70(1), 83.

Wolf, R.: 1861, Mitt. Sonnenflecken 2, 72.

Yua, K. K. and Stephenson, F. R.: 1988, Q. J. R. Astron. Soc. 29, 175